Задача
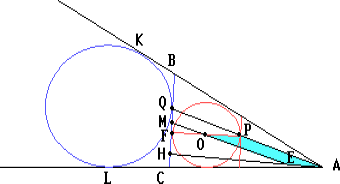
В треугольнике ABC через середину M стороны BC и центр O вписанной в этот треугольник окружности проведена прямая MO, которая пересекает высоту AH в точке E. Докажите, что отрезок AE равен радиусу вписанной окружности.
Решение
Пусть F — точка касания вписанной окружности треугольника ABC со стороной BC. Рассмотрим окружность S, касающуюся стороны BC треугольника ABC в точке Q, а продолжений сторон AB и AC — в точках K и L соответственно (вневписанная окружность треугольника ABC). Тогда, если p — полупериметр треугольника ABC, то
Поскольку MO — средняя линия треугольника QFP, то прямая ME параллельна прямой AP, а т.к. прямые PF и AH перпендикулярны прямой BC, то PO || AE. Поэтому четырёхугольник OPAE — параллелограмм. Следовательно, AE = OP = OF.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь