Задача
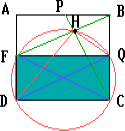
Дан квадрат ABCD. Точки P и Q лежат на сторонах AB и BC соответственно, причём BP = BQ. Пусть H – основание перпендикуляра, опущенного из точки B на отрезок PC. Докажите, что угол DHQ – прямой.
Решение
Пусть F – точка пересечения прямых AD и BH. Прямоугольные треугольники ABF и BCP равны по катету и острому углу. Поэтому AF = BP = BQ. Следовательно, QFDC – прямоугольник. Описанная около него окружность (FC – её диаметр) проходит через точку H, но DQ – также диаметр этой окружности. Поэтому ∠DHQ = 90°.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет