Задача
Дан правильный треугольник ABC. Некоторая прямая, параллельная прямой AC, пересекает прямые AB и BC в точках M и P соответственно. Точка D — центр правильного треугольника PMB, точка E — середина отрезка AP. Найдите углы треугольника DEC.
Решение
Первый способ.
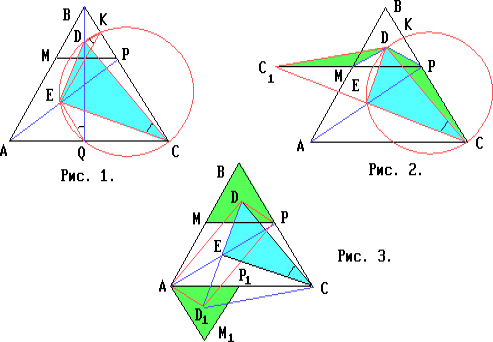
Пусть K — проекция точки D на
BC, а Q — проекция точки B на AC. Точки K, D, Q и C лежат на окружности
с диаметром CD. Поскольку
$\displaystyle \angle$EQD = $\displaystyle \angle$AQD - $\displaystyle \angle$AQE = 90o - 60o = 30o,
$\displaystyle \angle$DKE = $\displaystyle \angle$DKC - $\displaystyle \angle$EKC = 90o - $\displaystyle \angle$ABC = 90o - 60o = 30o,
то отрезокDEвиден из точекQиKпод одним и тем же углом.
Следовательно, точкиK,D,E,Qлежат на той же окружности.
Поэтому
$\displaystyle \angle$DEC = 90o, $\displaystyle \angle$DCE = $\displaystyle \angle$DQE = 30o.
Второй способ.
Пусть C1 — образ точки C при симметрии относительно точки E.
Треугольник C1DM равен треугольнику CDP, т.к.
C1M = C1P - MP = AC - MP = BC - BP = PC, MD = DP, $\displaystyle \angle$C1MD = $\displaystyle \angle$CPD = 150o.
ПоэтомуC1D=CD. Следовательно, медианаDEравнобедренного
треугольникаC1DCявляется его высотой.
ПустьK— середина отрезкаBP. ТогдаEK— средняя линия
треугольникаAPB, а т.к. точкиEиKлежат на окружности
с диаметромCD, то
$\displaystyle \angle$EDC = $\displaystyle \angle$EKC = 60o, $\displaystyle \angle$DEC = 90o, $\displaystyle \angle$DCE = 30o.
Третий способ.
Повернём треугольник BMP на
60o относительно точки C так,
чтобы точка B перешла в A. Тогда точка P перейдёт в точку P1
отрезка AC, точка M — в точку M1, лежащую вне треугольника ABC,
точка D — в точку D1, центр треугольника
AM1P1.
Четырехугольник DPD1A — параллелограмм, DD1 — его диагональ. Поэтому D1D проходит через точку E и D1E = DE.
Поскольку CE — медиана равнобедренного треугольника DCD1(CD = CD1), то $\angle$CED = 90o, а т.к. $\angle$DCD1 = 60o, то $\angle$DCE = 30o.
Ответ
90o, 60o, 30o.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет