Задача
Окружность S2 проходит через центр O окружности S1 и пересекает её в точках A и B. Через точку A проведена касательная к окружности S2. Точка D – вторая точка пересечения этой касательной с окружностью S1. Докажите, что AD = AB.
Решение
Отрезки OA, OB и OD равны как радиусы одной окружности. ∠ABO = ∠DAO по теореме об угле между касательной и хордой. Поэтому равнобедренные треугольники AOB и AOD равны Следовательно, AD = AB. 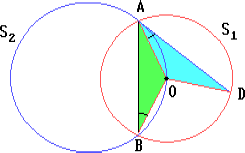
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет