Задача
Четырёхугольник ABCD, диагонали которого взаимно перпендикулярны, вписан в окружность с центром O. Найдите расстояние от точки O до стороны AB, если известно, что CD = 8.
Решение
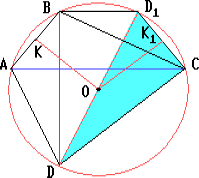
Проведём диаметр DD1. Пусть K и K1 — проекции точки O на хорды AB и CD1 соответственно. Поскольку BD1 и AC перпендикулярны DB, то BD1 параллельно AC. Поэтому D1C = AB и OK1 = OK.
Поскольку OK1 — средняя линия прямоугольного треугольника DD1C, то
OK = OK1 = $\displaystyle {\textstyle\frac{1}{2}}$DC = 4.
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет