Задача
Четырехугольник ABCD, диагонали которого взаимно перпендикулярны, вписан в окружность с центром O.
Докажите, что ломаная AOC делит его на две равновеликие части.
Решение
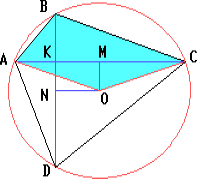
Решение 1:Пусть K – точка пересечения диагоналей AC и BD. Если O принадлежит AC, то решение очевидно. Иначе, один из получившихся четырёхугольников – выпуклый. Пусть тогда M и N – основания перпендикуляров, опущенных из точки O на AC и BD. Тогда
SABCO = ½ AC·OM + ½ AC·BK = ½ AC·(OM + BK) = ½ AC·(KN + BK) = ¼ AC·BD = ½ SABCD.
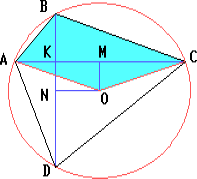
Решение 2:Пусть M – середина BD. OM || AC, поэтому SAOM = SCOM, и, значит, SAOCD = SAMCD. С другой стороны, SABM = SADM, SCBM = SCDM, следовательно, SAMCD = ½ SABCD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет