Решение 1:   Пусть QX и QY – высоты треугольников CQM и CQL, а PZ и PT – высоты треугольников CPK и CPN (рис. слева). Треугольники CQX и CPT подобны по двум углам. Также подобны треугольники CQY и CPZ с тем же коэффициентом подобия ^CQ/_CP. Поэтому   CQ : CP = QX : PT = QY : PZ.  Значит,

^CQ²/_CP² = ^OX/_PT ·^OY/_PZ = ^OX/_PZ ·^OY/_PT.

  Из равенства углов NKL и NML, а также MLK и MNK следует, что треугольник MXQ подобен треугольнику KZP, а треугольник LYQ – треугольнику NTP. Поэтому  ^OX/_PZ ·^OY/_PT = ^MQ/_KP ·^LQ/_NP.

  По теореме о равенстве произведений отрезков пересекающихся хорд

MQ·LQ = AQ·QB = (AC + CQ)(BC – CQ) = (AC + CQ)(AC – CQ) = AC² – CQ².   Аналогично  KP·NP = AC² – CP².

  Следовательно,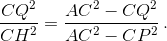  

  После перемножения и приведения подобных получим, что  CQ² = CP².

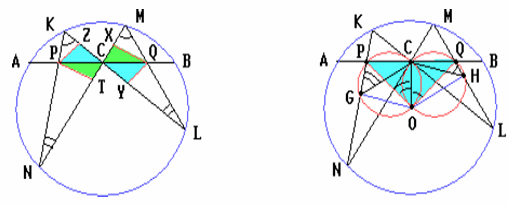
Решение 2:   Опустим из центра O данной окружности перпендикуляры OG и OH на хорды KN и ML соответственно (рис. справа). Тогда G и H – середины отрезков KN и ML. Рассмотрим случай, когда P и G – различные точки и Q и H – различные точки.

  Точки C и G лежат на окружности с диаметром OP, а точки C и H – на окружности с диаметром OQ. По теореме о вписанных углах  ∠COP = ∠CGP  и

∠COQ = ∠CHQ.  Поскольку треугольники KCN и MCL подобны, а CG и CH – их медианы, то подобны и треугольники KCG и MCH. Поэтому

∠CGP = ∠CHQ,  ∠COP = ∠COQ.

  Таким образом, высота CO треугольника POQ является его биссектрисой, а значит и медианой.

Решение 3:

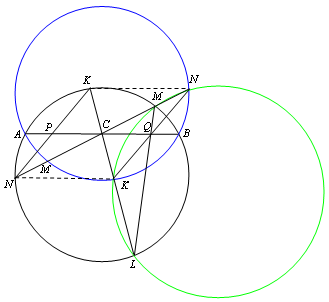
  Доказательство. При центральной симметрии угол KNM переходит в угол K'N'M'. Следовательно,  ∠K'LM = ∠KLM = ∠KNM = ∠K'N'M' = ∠K'N'M,  что и требовалось.  LM – общая хорда чёрной и зелёной окружностей, AB – чёрной и синей, K'N' – синей и зелёной. В силу теоремы о радикальном центре трёх окружностей), эти три отрезка пересекаются в одной точке, то есть точка Q лежит на отрезке K'N'. Таким образом, концы отрезка PQ лежат на противоположных сторонах параллелограмма KNK'N'. Поскольку точка C – центр симметрии этого параллелограмма, то она делит этот отрезок пополам.

Решение 4:   Рассмотрим проективное преобразование, которое окружность Ω переводит в окружность Ω', а точку С – в её центр O (см. задачу 158424 а)). Пусть A', B', ... – образы точек A, B, ... Тогда A'B', K'L' и M'N' – диаметры. Поэтому при центральной симметрии относительно O точка P' переходит в Q', то есть O – середина отрезка P'Q'. Так как хорда AB перпендикулярна диаметру, проходящему через С, то согласно задаче 158424 б) она параллельна исключительной прямой. Следовательно, согласно задаче 158422 б) отношения отрезков, лежащих на прямой AB, сохраняются, а значит, С – середина отрезка PQ.

Ответ задачи отсутствует