Задача
В треугольнике ABC угол B равен 60o, биссектрисы AD и CE пересекаются в точке O. Докажите, что OD = OE.
Решение
Поскольку
$\displaystyle \angle$EOD = $\displaystyle \angle$AOC = 180o - $\displaystyle {\textstyle\frac{1}{2}}$($\displaystyle \angle$BAC + $\displaystyle \angle$BCA) =
= 180o - $\displaystyle {\textstyle\frac{1}{2}}$ . 120o = 120o,
то точкиB,E,OиDлежат на одной окружности. Биссектрисы треугольника
пересекаются в одной точке, поэтомуBO— биссектриса углаDBE. Значит,
точкаO— середина дугиDOE. Следовательно,OD=OE.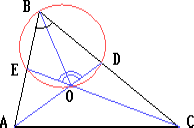
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет