Задача
В тетраэдре DABC ∠ACB = ∠ADB, ребро СD перпендикулярно плоскости АВС. В треугольнике АВС дана высота h, проведённая к стороне АВ, и расстояние d от центра описанной окружности до этой стороны. Найдите CD.
Решение
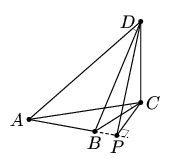
Пусть в тетраэдре DABC точка Р – основание перпендикуляра, опущенного на прямую АВ из точки С, тогда по теореме о трёх перпендикулярах DP ⊥ AB (рис. слева). Так как ∠ACB = ∠ADB, то равны и радиусы описанных окружностей граней ABC и ABD. Так как СD ⊥ (АВС), то эти грани не могут быть равными.
Рассмотрим треугольник АВС и треугольник АВD', равный треугольнику АВD, вписав их в одну окружность (рис. справа). Так как ∠ACB = ∠AD'B, то они расположены в одной полуплоскости относительно АВ. Кроме того, перпендикуляры, проведённые к прямой АВ из точек С и D', попадут в одну и ту же точку Р.

Ответ
2 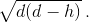
Чтобы оставлять комментарии, войдите или зарегистрируйтесь