Задача
Трапеция АВСD с основаниями AB и CD вписана в окружность. Докажите, что четырёхугольник, образованный ортогональными проекциями любой точки этой окружности на прямые AC, BC, AD и BD, является вписанным.
Решение
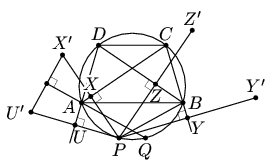
Пусть P – произвольная точка окружности, описанной около данной трапеции АВСD, X, Y, Z и U – ортогональные проекции точки P на AC, BC, BD и AD соответственно (см. рис.). Так как трапеция вписана в окружность, то она – равнобокая. Пусть Q – точка, симметричная P относительно оси симметрии трапеции, тогда ∠QAC = ∠PBD.
Рассмотрим точки X', Y', Z' и U', симметричные P относительно сторон трапециих. Так как четырёхугольник AXPU вписанный,
∠UXP = ∠UAP = ∠PBD = ∠QAC. Поэтому ∠QAX + ∠UXА = ∠QAC + ∠UXА = ∠UXP + ∠UXА = 90°, то есть AQ ⊥ UX. Значит, AQ ⊥ U'X', и, так как
AU' = AP = AX', то AQ – серединный перпендикуляр к отрезку X'U'.
Аналогично доказывается, что серединные перпендикуляры к отрезкам X'Z' и Y'Z' проходят через Q. Следовательно, четырёхугольник с вершинами X', Y', Z' и U' вписан в окружность с центром Q. Так как четырёхугольник с вершинами X, Y, Z и U получается из него гомотетией с центром Р и коэффициентом ½, то он также будет вписанным.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь