Задача
В треугольнике АВС М – точка пересечения медиан, О – центр вписанной окружности.
Докажите, что если прямая ОМ параллельна стороне ВС, то точка О равноудалена от середин сторон АВ и АС.
Решение
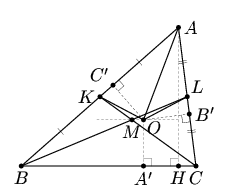
Пусть K и L – середины сторон АВ и АС, AH – высота, A', B' и C' – точки касания окружности со сторонами высота треугольника АВС, r – радиус этой окружности (см. рис.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет