Задачи и олимпиады по математике

Задача

На доске была нарисована окружность с отмеченным центром, вписанный в неё четырёхугольник и окружность, вписанная в него, также с отмеченным центром. Затем стерли четырёхугольник (сохранив одну вершину) и вписанную окружность (сохранив её центр). Восстановите какую-нибудь из стертых вершин четырёхугольника, пользуясь только линейкой и проведя не более шести линий.

Решение

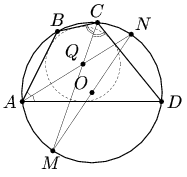
Рассмотрим исходный чертёж: ABCD – данный четырёхугольник; О и Q – центры описанной и вписанной окружностей соответственно (см. рис.).

Заметим, чтоAQ– биссектриса углаBAD; пусть она пересекает описанную окружность в точкеN. Значит, ⌣BN= ⌣ND. ПустьMN– диаметр окружности, тогда ⌣BM= ⌣MD. Следовательно,СМ– биссектриса углаBCD, поэтому она содержит центрQвписанной окружности. Таким образом, если на чертеже сохранилась, например, вершинаА, то можно восстановить противолежащую вершинуС. Для этого достаточно провеститри линии: лучAQдо пересечения с описанной окружностью в точкеN, лучNOдо пересечения с описанной окружностью в точкеMи лучMQдо пересечения с описанной окружностью в искомой точкеС.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления