Задача
Треугольник ABC вписан в окружность. Через точки A и B проведены касательные к этой окружности, которые пересекаются в точке P. Точки X и Y — ортогональные проекции точки P на прямые AC и BC. Докажите, что прямая XY перпендикулярна медиане треугольника ABC, проведенной из вершины C.
Решение
Тогда ∠PXY = ∠ACD; ∠PYX = ∠BCD.
Следовательно,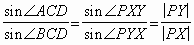 
.
Кроме того, так как |PA| = |PB|, то 
.
.
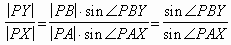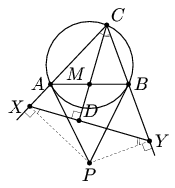
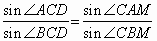Используя теорему синусов для треугольников АВМ и СВМ, получим:
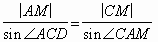и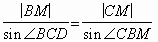 
.
Следовательно, 
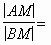1, то есть,
CM — медиана треугольника ABC, ч. т. д.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет