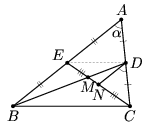
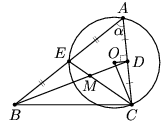
Пусть треугольник АВС с данными медианами ВD и CE и углом А, имеющим величину α, построен (см. рис. а, б). М — точка пересечения медиан.Первый способ. Заметим, что точка А принадлежит геометрическому месту точек, из которых отрезок СE виден под данным углом α (дуга окружности с центром О, см. рис. а). Кроме того, |CM| : |ME| = 2 : 1 и 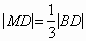. Так как D — середина хорды АС, то ∠ODC = 90°. Следовательно, точка D лежит на пересечении окружности с центром М и радиусом 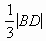и окружности с диаметром ОС. Таким образом, искомое построение сводится к построению отрезка СЕ; ГМТ из которых этот отрезок виден под углом α (тем самым построена и точка О); точки М и точки D пересечения двух ранее указанных ГМТ. Вершина А является пересечением луча CD c первым из построенных ГМТ, а вершина В — пересечением лучей АЕ и DM. Второй способ. Пусть N — середина медианы CE (см. рис. б). Тогда ∠NDC = ∠BAC = α. Поэтому, точка D лежит на пересечении двух геометрических мест точек: ГМТ, из которых отрезок CN виден под углом α и ГМТ, удаленных от точки M на расстояние, равное 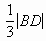. Построив точку D, мы получим треугольник CED. Так как ED — средняя линия треугольника АВС, то из треугольника CED несложно восстановить треугольник ABC.

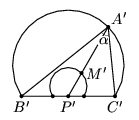
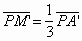Третий способ. Построим сначала некоторый треугольник A'B'C', подобный искомому. Для этого выберем произвольный отрезок B'C' и построим геометрическое место точек, из которых он виден под данным углом α (см. рис. в). Пусть P' — середина B'C'. Так как , где M' — центр тяжести треугольника A'B'C', то точка M' должна лежать на дуге, которая получается из построенной гомотетией с центром P' и коэффициентом 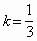. С другой стороны, так как 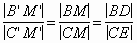, то M' лежит на окружности Аполлония точек B' и C'. Следовательно, M' является пересечением указанной дуги и этой окружности. Зная положение точки М', восстанавливаем треугольник A'B'C'. Искомый треугольник АВС получается из него преобразованием подобия с коэффициентом, равным .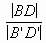

Ответ задачи отсутствует