Задача
В выпуклом четырехугольнике АВСD точка Е — середина CD, F — середина АD, K — точка пересечения АС и ВЕ. Докажите, что площадь треугольника BKF в два раза меньше площади треугольника АВС.
Решение
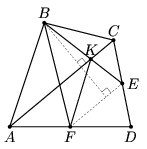
Первый способ. Проведем EF — среднюю линию треугольника ADC
(см. рис. а). Тогда 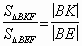 , так как высоты этих треугольников,
проведенные из вершины F, совпадают. Кроме того, так как (EF) || (AC),
то длины перпендикуляров, опущенных из точки В на прямые EF и AC относятся,
как |BE| : |BK|, поэтому,
, так как высоты этих треугольников,
проведенные из вершины F, совпадают. Кроме того, так как (EF) || (AC),
то длины перпендикуляров, опущенных из точки В на прямые EF и AC относятся,
как |BE| : |BK|, поэтому, 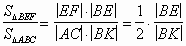 .
Перемножив почленно полученные равенства, имеем:
.
Перемножив почленно полученные равенства, имеем: 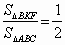 ,
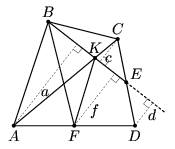
ч. т. д.Второй способ. Пусть a, c, f и d —
длины перпендикуляров, опущенных на прямую BЕ из точек A, C, F и D соответственно
(см. рис. б). Тогда c = d;
,
ч. т. д.Второй способ. Пусть a, c, f и d —
длины перпендикуляров, опущенных на прямую BЕ из точек A, C, F и D соответственно
(см. рис. б). Тогда c = d; 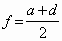 .
Следовательно,
.
Следовательно, 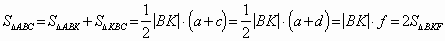 , ч. т. д.
, ч. т. д.
 |
 |
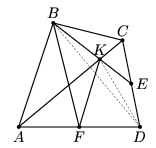 |
| Рис. а | Рис. б | Рис. в |
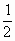 SΔBСD
и SΔABF =
SΔBСD
и SΔABF =
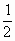 SΔABD. Кроме того, так как EF — средняя
линия треугольника ADC, то SΔDEF =
SΔEFK =
SΔABD. Кроме того, так как EF — средняя
линия треугольника ADC, то SΔDEF =
SΔEFK = 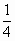 SΔACD. Следовательно, SΔBKF =
SABCD — SΔABF —
SΔBCE —
SDFKE =
SΔACD. Следовательно, SΔBKF =
SABCD — SΔABF —
SΔBCE —
SDFKE = 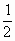 (SΔABD + SΔBCD +
SΔACD) =
(SΔABD + SΔBCD +
SΔACD) =
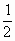 SΔABC, ч. т. д.
SΔABC, ч. т. д.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь