Задача
Докажите, что число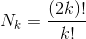 
делится на 2k и не делится на 2k+1.
Решение
Докажем утверждение индукцией по k. База (k = 1) очевидна.
Шаг индукции.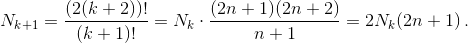 
Таким образом, число Nk+1 получается из Nk домножением на 2 и на нечётное число, поэтому по предположению индукции оно делится на на 2k+1 и не делится на 2k+2.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет