Задачи и олимпиады по математике

Задача

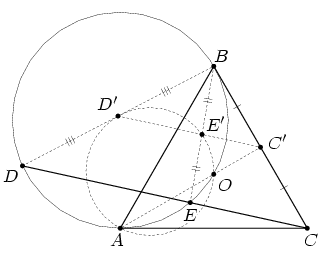
Дан правильный треугольник ABC с центром O. Прямая, проходящая через вершину C, пересекает описанную окружность треугольника AOB в точках D и E. Докажите, что точки A, O и середины отрезков BD, BE лежат на одной окружности.

Решение

Пусть C' – середина BC, а E лежит между С и D. Тогда точка E' (середина BE) лежит на средней линии C'D' треугольника CBD.

В правильном треугольнике ABC вершина A, центр O и точка C' также лежат на одной прямой. Угол ABC равен половине дуги AOB, поэтому BC – касательная. Тогда C'E'·C'D' = ¼ CE·CD = ¼ CB² = С'B² = C'O·C'A. Отсюда по теореме, обратной к теореме о произведении отрезков секущих, и следует вписанность четырёхугольника AOE'D'.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления