Назад
Задача 132899 • Сложность: 2 • 9-11 класс
Задача

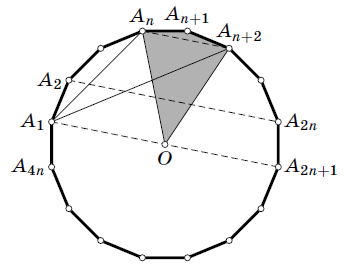
Дан правильный 4n-угольник A1A2...A4n площади S, причём  n > 1.  Найдите площадь четырёхугольника A1AnAn +1An+2.

Авторы:
Ивлев Ф. Николаев С. А.
Разделы:
Планиметрия
Источники:
Московская математическая олимпиада Олимпиады и турниры 2013 год
Количество версий:
3
Решение

A1 и A2n+1 – противоположные вершины многоугольника. Следовательно, диагональ A1A2n+1 проходит через центр O (см. рисунок).

В силу равенства дуг A1An и An+2A2n+1 описанной окружности  A1A2n+1 || AnAn+2.  Значит, площади треугольников A1AnAn+2 и OAnAn +2 равны. Отсюда  SA1AnAn+1An+2 = SOAnAn+1An+2 = S/2n .

Ответ

S/2n.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет