Задача
На плоскости даны две окружности одна внутри другой. Построить такую точку O, что одна окружность получается из другой гомотетией относительно точки O (другими словами – чтобы растяжение плоскости от точки O с некоторым коэффициентом переводило одну окружность в другую).
Решение
Пусть O – искомая точка, A1 и B1 – две диаметрально противоположные точки внутренней окружности, A2 и B2 – соответствующие точки внешней окружности. Ясно, что прямые A1B1 и A2B2 параллельны.
Отсюда следует искомое построение: через центры Q1 и O2 окружностей ω1 и ω2 проводим параллельные (но не совпадающие) прямые l1 и l2; точки пересечения прямой l1 с окружностью ω1 обозначаются A1 и B1, а прямой l2 с окружностью l2 – A2 и B2. Точка пересечения прямых A1A2 и B1B2 и будет искомой точкой O (см. рис.).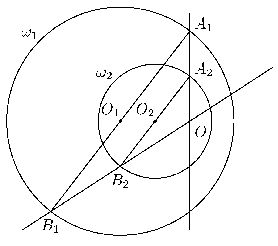
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь