Задача
Вершины A, B, C треугольника соединены с точками A1, B1, C1, лежащими на противоположных сторонах (не в вершинах).
Могут ли середины отрезков AA1, BB1, CC1 лежать на одной прямой?
Решение
Средняя линия B2C2 треугольника ABC параллельна основанию BC. Отсюда следует, что эта прямая содержит среднюю линию треугольника CAA1. Поэтому середина отрезка AA1 лежит на отрезке B2C2. Аналогично середины отрезков BB1 и CC1 лежат на двух других средних линиях треугольника ABC (см. рис.). Поскольку прямая не может пересекать три стороны треугольника во внутренних точках, три указанные точки не могут лежать на одной прямой. 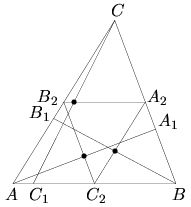
Ответ
Не могут.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет