Задача
В треугольнике ABC на стороне AB выбрана точка D
такая, что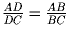 ,.
Докажите, что угол C — тупой.
,.
Докажите, что угол C — тупой.
Решение
Теорема синусов, примененная к треугольникам
ABC и ADC, дает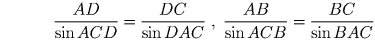 или
или Учитывая условие задачи и то, что углы DAC и BAC равны,
получаем
sin ACD = sin ACB.
Так как углы ACB и ACD не равны, то последнее равенство
означает, что их сумма равна 180. Значит, больший из них
— угол ACB — тупой.
Учитывая условие задачи и то, что углы DAC и BAC равны,
получаем
sin ACD = sin ACB.
Так как углы ACB и ACD не равны, то последнее равенство
означает, что их сумма равна 180. Значит, больший из них
— угол ACB — тупой.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет