При центральной симметрии относительно середины отрезка один его конец переходит в другой. На этом очевидном замечании и базируется требуемое построение. Отобразим одну из данных окружностей симметрично относительно данной точки (см. рис.). Точка пересечения образа этой окружности со второй окружностью и будет концом искомого отрезка. Отразив один конец относительно середины, находим второй конец.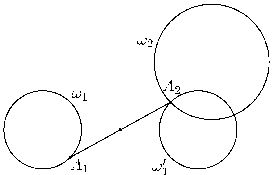Задача может не иметь решений или иметь одно, два или бесконечно много решений в зависимости от количества точек пересечения образа первой окружности со второй окружностью (бесконечно много решений будет в случае, если данные окружности симметричны относительно данной точки). (Если данные окружности совпадают, то решений бесконечно много когда точка – их центр, решение единственно для любой другой точки внутри окружностей, и решений нет для точки вне их.)

Ответ задачи отсутствует