Задача
Пусть p и q – различные простые числа. Докажите, что
а) pq + qp ≡ p + q (mod pq); б)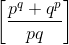 
– чётное число, если p, q ≠ 2.
Решение
а) По малой теореме Ферма pq ≡ p (mod q), qp ≡ q (mod p). Следовательно, pq + qp – p – q делится и на p, и на q. б) p + q < pq, поэтому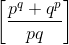 
Числитель полученной дроби чётен, а знаменатель нет, следовательно, частное чётно.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет