Олимпиадная задача по планиметрии для 5–7 классов: угол PIQ в треугольнике

Решение 1:   Заметим, что  ∠ABQ = ∠CBP = ∠ABI = ∠CBI = 60°.

  Пусть  ∠BAC= 2x,  а  ∠BCA= 2y,  тогда (из треугольникаABC)  2x+ 2y+ 120° = 180°,  то есть  x + y= 30°.   ТреугольникиACIиQCIравны (по первому признаку), поэтому  ∠CQI= ∠CAI = x.  Из треугольникаQBI:  ∠QIB= 180° – 120° –x= 60° –x. Аналогично  PIB= 60° –y.   Таким образом,  ∠PIQ= ∠PIB+ ∠QIB= (60° –y) + (60° –x) = 120° – (x + y) = 120° – 30° = 90°.

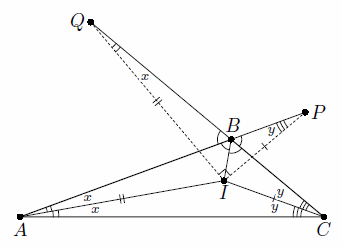
Решение 2:   Пусть биссектриса CI пересекает AQ в точке M (см. рис.).

Эта биссектриса – ось симметрии углаC, точкиAиQсимметричны относительно неё, значит, углыAIMиQIMравны.   ∠AIC= 90° + 60° = 150°  (см. задачу155448), поэтому  ∠AIM= 30°,  а  ∠AIQ= 2∠AIM= 60°.   Аналогично  ∠CIP= 60°,  и  ∠PIQ= 180° – ∠MIQ– ∠CIP= 180° – 30° – 60° = 90°.

Ответ задачи отсутствует