Олимпиадная задача по стереометрии: вычисление расстояния в цилиндре для 9–11 классов
Задача
Точка А лежит на окружности верхнего основания прямого кругового цилиндра (см. рис.), В – наиболее удалённая от неё точка на окружности нижнего основания, С – произвольная точка окружности нижнего основания. Найдите АВ, если АС = 12, BC = 5.
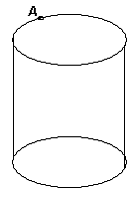
Решение
Пусть А' – ортогональная проекция точки А на нижнее основание цилиндра, а В' – произвольная точка окружности этого основания (см. рисунок), тогда АB'² = А'A² + А'B'².
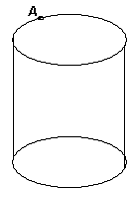
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет