Олимпиадная задача по планиметрии: площадь треугольника с углом 60° и симметричной точкой D
Задача
В треугольнике ABC угол B равен 60°. Точка D внутри треугольника такова, что ∠ADB = ∠ADC = ∠BDC.
Найдите наименьшее значение площади треугольника ABC, если BD = a.
Решение
Из условия следует, что ∠ADB = ∠ADC = ∠BDC = 120° (см. рисунок).

AD : BD = BD : CD, то есть AD·CD = BD² = a². Значит, SADC = AD·CD·sin 120° – величина постоянная.
Таким образом, площадь треугольника АВС будет наименьшей, если будет наименьшей сумма площадей треугольников ADB и BDC. Но
SADB + SBDC = ½ a(AD + CD) sin 120°, а сумма AD + CD минимальна, когда треугольник ADC равнобедренный (см. задачу 132883 б).
В этом случае, очевидно, треугольник АВС равносторонний и 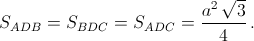
Ответ
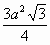 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет