Олимпиадная задача: какие размеры куба n возможны при особой раскраске?
Задача
Куб с ребром n составлен из белых и чёрных кубиков с ребром 1 таким образом, что каждый белый кубик имеет общую грань ровно с тремя чёрными, а каждый чёрный – ровно с тремя белыми. При каких n это возможно?
Решение
Количество "соприкосновений" чёрных и белых граней в три раза больше как количества чёрных, так и количества белых кубиков. Следовательно, количество чёрных кубиков равно количеству белых и общее число кубиков чётно.
Построим теперь куб с ребром 2, удовлетворяющий условию задачи. Для этого нижний слой 2×2 уложим в шахматном порядке, а верхний – также в шахматном порядке, но с противоположной раскраской (см. рис.). Любой куб с чётной длиной ребра, удовлетворяющий условию, можно собрать из таких кубиков с ребром 2, прикладывая их друг к другу гранями с одинаковой раскраской.
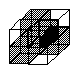
Ответ
При всех чётных n.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь