Олимпиадная задача по планиметрии: сумма трёх векторов и модуль суммы пар
Задача
Можно ли расположить на плоскости три вектора так, чтобы модуль суммы каждых двух из них был равен 1, а сумма всех трёх была равна нулевому вектору?
Решение
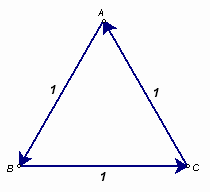
Заметим, что если сумма трёх единичных векторов равна нулю, то сумма каждых двух из них равна третьему с обратным знаком, то есть её модуль равен 1. Три таких единичных вектора можно расположить по разному. Первый способ. Рассмотрим правильный треугольник АВС
со сторонами единичной длины (см. рис.). Тогда искомый пример: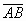 
, 
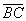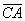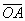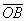и 
.
, 
и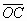 
, образующие попарно углы 120° (см. задачу 155373 а).
Ответ
Можно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет