Оригинальная олимпиадная задача Блинкова: футбольный турнир и минимум команд
Задача
Команды провели турнир по футболу в один круг (каждая с каждой сыграла один раз, победа – 3 очка, ничья – 1, поражение – 0). Оказалось, что единоличный победитель набрал менее 50% от количества очков, возможного для одного участника. Какое наименьшее количество команд могло участвовать в турнире?
Решение
Докажем, что команд не могло быть менее шести. Если в турнире участвовало, например, пять команд, то они провели между собой 5·4 : 2 = 10 матчей и в сумме набрали не менее 20 очков. Значит, единоличный победитель набрал более 20 : 5 = 4 очков. Но по условию он набрал не более 5 очков из 12 возможных. Следовательно, победитель набрал ровно 5 очков, а каждая из остальных команд – не более 4. Таким образом, сумма очков, набранных всеми участниками, не превосходит 5 + 4·4 = 21. Но количество очков, набранных победителем, означает, что он хотя бы один раз выиграл и хотя бы один раз проиграл, то есть в этом случае сумма очков, набранных всеми командами не может быть меньше 22. Противоречие.
Рассуждения для турнира из двух, трех или четырёх команд аналогичны.
Приведём два возможных примера для турнира, в котором участвовали шесть команд:
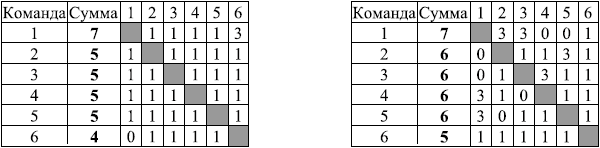
Ответ
6 команд.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь