Олимпиадная задача о трех муравьях и квадратных дорожках — планиметрия 6-8 класс
Задача
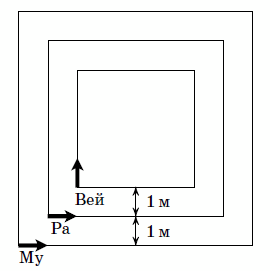
Три квадратные дорожки с общим центром отстоят друг от друга на 1 м (см. рис.). Три муравья стартуют одновременно из левых нижних углов дорожек и бегут с одинаковой скоростью: Му и Ра против часовой стрелки, а Вей по часовой. Когда Му добежал до правого нижнего угла большой дорожки, двое других, не успев ещё сделать полного круга, находились на правых сторонах своих дорожек, и все трое оказались на одной прямой. Найдите стороны квадратов.
Решение
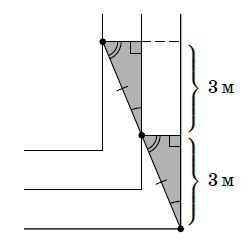
Длины сторон двух соседних дорожек отличаются на 2 м. Поэтому в момент, когда Му добежал до угла, Ра пробежал по правой стороне дорожки 2 м и находился на расстоянии 2 + 1 = 3 м от "нижней" стороны внешней дорожки. Поскольку Ра находится посредине между Му и Веем, Вей в этот момент находится на вдвое большем расстоянии от этой стороны, 6 м. То есть Вею остаётся ещё пробежать по боковой стороне 6 – 1 – 1 = 4 м.
Ответ
4 м, 6 м, 8 м.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь