Олимпиадная задача по математической логике и делимости для 5–7 класса: мальчики и девочки за столом
Задача
13 детей сели за круглый стол и договорились, что мальчики будут врать девочкам, а друг другу говорить правду, а девочки, наоборот, будут врать мальчикам, а друг другу говорить правду. Один из детей сказал своему правому соседу: "Большинство из нас мальчики". Тот сказал своему правому соседу: "Большинство из нас девочки", а он своему соседу справа: "Большинство из нас мальчики", а тот своему: "Большинство из нас девочки" и так далее, пока последний ребёнок не сказал первому: "Большинство из нас мальчики". Сколько мальчиков было за столом?
Решение
Понятно, что за столом были и мальчики, и девочки. За группой сидящих рядом мальчиков следует группа девочек, затем снова мальчики, снова девочки и так далее (группа может состоять и из одного человека). Группы мальчиков и девочек чередуются, поэтому их чётное число. Неверные утверждения звучали на переходах от группы к группе, то есть их тоже чётное число. Так как утверждений "большинство из нас мальчики" прозвучало семь, то неверны шесть утверждений "большинство из нас девочки", и групп тоже было шесть.
Чередование верных и неверных утверждений означает, что в группах было по двое детей. Лишь сидящие рядом первый и последний ребенок сказали одно и то же, поэтому в их группе три человека. Это мальчики, так как их большинство. Всего за столом сидели 2 + 2 + 2 = 6& девочек и 2 + 2 + 3 = 7 мальчиков.
(На рисунке показано, как именно ребята сидели за столом. Первый говорящий обведён в рамочку.)
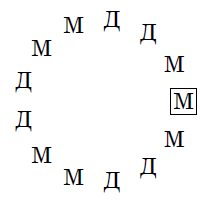
Ответ
7 мальчиков.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь