Назад

Олимпиадная задача по планиметрии для 8-10 классов: деление отрезка в треугольнике

Задача 216950 • Сложность: 3 • 8-10 класс
Задача

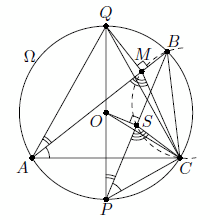
В окружность Ω вписан остроугольный треугольник ABC, в котором  AB > BC.  Пусть P и Q – середины меньшей и большей дуг AC окружности Ω, соответственно, а M – основание перпендикуляра, опущенного из точки Q на отрезок AB. Докажите, что описанная окружность треугольника BMC делит пополам отрезок BP.

Авторы:
Ивлев Ф.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 2012-2013 Региональный этап
Количество версий:
4
Решение

  Пусть S – середина хорды BP, O – центр окружности Ω.   Первый способ. Равнобедренные треугольники AQC и POC подобны, так как углы QAC и OPC опираются на одну дугу QC. Прямоугольные треугольники AQM и POS подобны, так как углы QAM и OPS опираются на одну дугу QB. Поэтому  AM : PS = AQ : PO = AC : PC.

  Поскольку углы MAC и SPC опираются на одну дугу BC, то треугольники AMC и PSC подобны. Отсюда следует, что углы BMC и BSC равны как смежные с соответственными углами в этих треугольниках. Следовательно, точки B, C, M, S лежат на одной окружности.

  Второй способ. Пусть K – точка, симметричная точке C относительно прямой BQ. Прямая BQ является внешней биссектрисой угла ABC, значит, точка K лежит на прямой AB. Далее, из симметрии получаем  QK = QC = QA.  Значит, треугольник QAK равнобедренный, и его высота QM является медианой:  AM = MK.

  Но и треугольник BCK равнобедренный, значит,  ∠BKC = ½ ∠ABC = ∠PBC.  Кроме того, углы BPC и BAC равны как опирающиеся на одну дугу. Следовательно, треугольники CAK и CPB подобны. Поэтому углы CSB и CMK (соответственные в этих подобных треугольниках) равны, то есть  

CSB = ∠CMB.  Значит, точки C, S, M, B лежат на одной окружности.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет