Олимпиадная задача по многочленам: равенство дискриминантов, 8–10 класс

  Пусть a₁ и a₂ – корни трёхчлена P(x), а b₁ и b₂ – корни трёхчлена Q(x).   Первый способ.  P(x) = (x – a₁)(x – a₂),  Q(x) = (x – b₁)(x – b₂).  Поэтому  (b₁ – a₁)(b₁ – a₂) + (b₂ – a₁)(b₂ – a₂) = (a₁ – b₁)(a₁ – b₂) + (a₂ – b₁)(a₂ – b₂). Перенося все слагаемые в одну часть, получаем  (b₁ – a₁)(b₁ – a₂ + a₁ – b₂) + (b₂ – a₂)(b₂ – a₁ + a₂ – b₁) = 0,  то есть

(b₁ – b₂)² – (a₁ – a₂)² = (b₁ + a₂ – a₁ – b₂) (a₁ + b₁ – a₂ – b₂) = 0.

  Но  (b₁ – b₂)²  и  (a₁ – a₂)²  как раз и есть дискриминанты данных трёхчленов.   Второй способ. Пусть  P(x) = x² + px + r,  Q(x) = x² + qx + s.  Тогда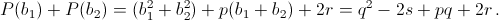  

  Аналогично  Q(a₁) + Q(a₂) = p² – 2r + pq + 2s.

  По условию  p² – 2r + pq + 2s = q² – 2s + pq + 2r,  откуда  p² – 4r = q² – 4s.

Ответ задачи отсутствует