Олимпиадная задача по планиметрии для 8-10 классов от Емельянова Л. А.
Задача
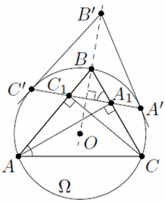
В остроугольном треугольнике ABC проведены высоты AA1 и CC1. Описанная окружность Ω треугольника ABC пересекает прямую A1C1 в точках A' и C'. Касательные к Ω, проведённые в точках A' и C', пересекаются в точке B'. Докажите, что прямая BB' проходит через центр окружности Ω.
Решение
Угол BA1C1 (совпадающий с BA1C') измеряется полусуммой дуг BC' и CA', а равный ему угол A (см. задачу 152537) – половиной дуги BC. Значит, дуги BA' и BC' равны. Поэтому точки B' и B лежат на серединном перпендикуляре к хорде A'C' окружности Ω. Центр окружности Ω также лежит на этом серединном перпендикуляре.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет