Олимпиадная задача по планиметрии для 8–10 класса. Серединные перпендикуляры треугольника
Задача
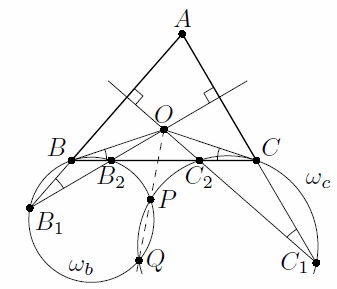
Серединный перпендикуляр к стороне AC неравнобедренного остроугольного треугольника ABC пересекает прямые AB и BC в точках B1 и B2 соответственно, а серединный перпендикуляр к стороне AB пересекает прямые AC и BC в точках C1 и C2 соответственно. Описанные окружности треугольников BB1B2 и CC1C2 пересекаются в точках P и Q. Докажите, что центр описанной окружности треугольника ABC лежит на прямой PQ.
Решение
Пусть O – центр описанной окружности треугольника ABC. Покажем сначала, что прямая OB касается описанной окружности ωb треугольника BB1B2.
Пусть AB < BC; тогда точка B2 лежит на стороне BC, а B1 – на продолжении стороны AB за точку B. Имеем ∠B2B1A = ∠OB1A = 90° – ∠A. С другой стороны, ∠B2BO = ∠CBO = 90° – ½ ∠BOC = 90° – ∠A. Таким образом, вписанный угол B2B1B равен углу между секущей BB2 и прямой OB. Следовательно, OB касается ωb.
Если AB > BC, то проходит то же рассуждение с заменой точки A на C и наоборот.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь