Олимпиадная задача по многочленам для 8–10 класса от Агаханова Н. Х.

Решение 1:   Пусть  |b| ≠ |a|.  Тогда  b + a ≠ 0,  и данное уравнение  (a + b)x² – 2(a² + b²)x + (a³ + b³) = 0  – квадратное. При этом

^D/₄ = (a² + b²)² – (a + b)(a³ + b³) = – ab(a – b)² ≠ 0.  Значит, уравнение не может иметь ровно одно решение. Противоречие.

Решение 2:   Пусть числа a и b одного знака. Если они оба положительны, то  a(x – a)² + b(x – b)² = 0  только в случае, когда  a(x – a)² = 0  и  b(x – b)² = 0,  то есть

a = x = b.  Аналогично рассматривается случай, когда оба числа отрицательны (знаки неравенств меняются на противоположные).

  Пусть, например,  a > 0 > b.  Тогда  a = c², b = – d²,  где  c > 0  и  d > 0.  Имеем

0 = a(x – a)² + b(x – b)² = c²(x – a)² – d²(x – b)² = (c(x – a) – d(x – b))(c(x – a) + d(x – b)).  Если  c ≠ d,  полученное уравнение имеет два различных корня 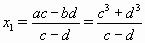    и 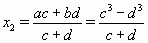   (|x₂| < |x₁|,  поскольку  |c³ + d³| > |c³ – d³|  и  |c – d| < |c + d|).  Значит,  c = d,  откуда  b = – a.

Ответ задачи отсутствует