Олимпиадная задача по планиметрии: центр вписанной окружности и высота в треугольнике (Агаханов Н. Х.)
Задача
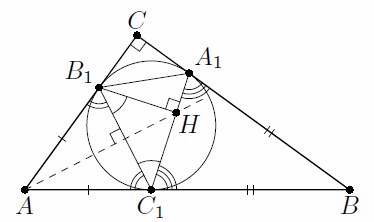
Окружность, вписанная в прямоугольный треугольник ABC с гипотенузой AB, касается его сторон BC, CA, AB в точках A1, B1, C1 соответственно. Пусть B1H – высота треугольника A1B1C1. Докажите, что точка H лежит на биссектрисе угла CAB.
Решение
Из равнобедренных треугольников AB1C1 и BA1C1 имеем ∠AC1B1 = 90° – ½ ∠BAC и ∠BC1A1 = 90° – ½ ∠ABC, поэтому
∠A1C1B1 = 180° – ∠AC1B1 – ∠BC1A1 = ½ (∠BAC + ∠ABC) = 45°.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет