Назад

Олимпиадная задача по планиметрии и проективной геометрии для 9-10 класса — доказательство коллинеарности ортоцентров в квадрате

Задача 216918 • Сложность: 4 • 9-10 класс
Задача

На стороне BC квадрата ABCD выбрали точку M. Пусть X, Y, Z – центры окружностей, вписанных в треугольники ABM, CMD, AMD соответственно; Hx, Hy, Hz – ортоцентры треугольников AXB, CYD, AZD соответственно. Докажите, что точки Hx, Hy, Hz лежат на одной прямой.

Решение

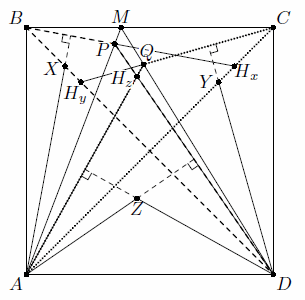
  Точки X и Y лежат на диагоналях BD и AC соответственно; поэтому прямые AC и BD содержат высоты треугольников AXB и CYD. Отметим на отрезках AM и DM точки P и Q так, что  AP = DQ = AD.  Тогда AX – биссектриса и, следовательно, высота в равнобедренном треугольнике ABP; значит, ортоцентр Hx – это точка пересечения прямых BP и AC. Аналогично Hy – точка пересечения CQ и BD. Из тех же соображений получаем  AZ ⊥ DP,

DZ ⊥ AQ,  так что Hz – точка пересечения прямых AQ и DP (см. рис.).

  Применимтеорему Дезаргак треугольникамBPDиCAQ: прямыеBC, PAиDQ, соединяющие их соответственные вершины, пересекаются в точкеM, следовательно, точки пересечения прямых, содержащих соответственные стороны этих треугольиков, лежат на одной прямой. Как показано выше, эти точки и естьHx, HyиHz.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет