Олимпиадная задача по планиметрии для 9-10 класса: касательные окружности, треугольник ABC, автор Ивлев Ф.
Задача
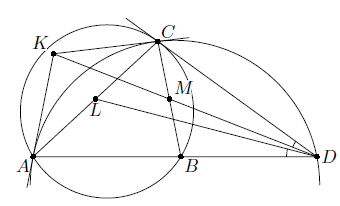
Дан треугольник ABC. Касательная в точке C к его описанной окружности пересекает прямую AB в точке D. Касательные к описанной окружности треугольника ACD в точках A и C пересекаются в точке K. Докажите, что прямая DK делит отрезок BC пополам.
Решение
Прямая DK является симедианой треугольника ACD (см. задачу 156983). Треугольники ACD и CBD подобны. Значит, если DL и DM – их медианы, то ∠CDK = ∠ADL = ∠CDM, откуда и следует, что точка M лежит на DK.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет