Назад

Олимпиадная задача: равенство радиусов вписанных окружностей в луночках, планиметрия, 9-10 класс

Задача 216915 • Сложность: 2 • 9-10 класс
Задача

В окружность Ω вписан четырёхугольник ABCD, диагонали AC и BD которого перпендикулярны. На сторонах AB и CD во внешнюю сторону как на диаметрах построены дуги α и β. Рассмотрим две луночки, образованные окружностью Ω и дугами α и β (см. рис.). Докажите, что максимальные радиусы окружностей, вписанных в эти луночки, равны.

Авторы:
Нилов Ф.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина VIII Олимпиада по геометрии имени И.Ф. Шарыгина (2012 г.)
Количество версий:
5
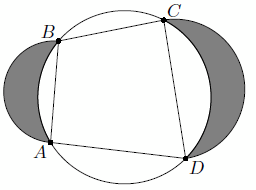
Решение

   Пусть X и Y – середины дуги α и дуги AB окружности Ω соответственно, а O – центр Ω. Тогда луночка с вершинами A и B находится между концентрическими окружностями с центром O и радиусами OY и OX (см. рис.). Значит, диаметр окружности, вписанной в луночку, не превосходит XY; с другой стороны, окружность с диаметром XY касается Ω и α и лежит в луночке. Итак, максимальный диаметр окружности, вписанной в эту луночку, равен XY.

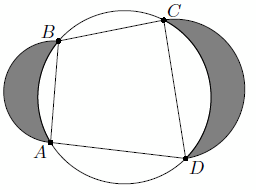
  Поскольку  AC⊥BD,  сумма дугABиCDокружности Ω равна 180°. ПустьKиL– середины отрезковABиCDсоответственно; тогда ∠AOK= 90° – ∠COL= ∠OCL,  поэтому прямоугольные треугольникиAOKиOCLравны по гипотенузе и острому углу. Значит, OX = OK + KX = OK + KA= ½ (AB + CD),  поэтому  XY= ½ (AB + CD) –r,  гдеr– радиус Ω.   Аналогично максимальный диаметр окружности, вписанной в луночку с вершинамиCиDтакже равен  ½ (AB + CD) –r.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет