Олимпиадная задача: максимальное число хороших точек и свойства треугольника

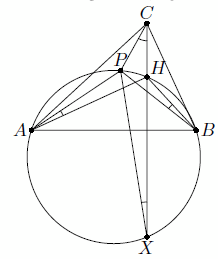
  Пусть AA₁, BB₁, CC₁ – высоты треугольника ABC, H – его ортоцентр. Рассмотрим любую хорошую точку P; пусть AA_p, BB_p, CC_p – проходящие через неё чевианы. Тогда  AA_p : AA₁ = BB_p : BB₁ = CC_p : CC₁;  значит, прямоугольные треугольники AA₁A_p, BB₁B_p и CC₁C_p подобны, поэтому

∠A₁AA_p = ∠B₁BB_p = ∠C₁CC_p.  При этом возможны два различных случая ориентации этих углов. (Напомним, что ориентированным углом  ∠(l, m)  называется угол, на который надо повернуть против часовой стрелки прямую l, чтобы она стала параллельна m.)

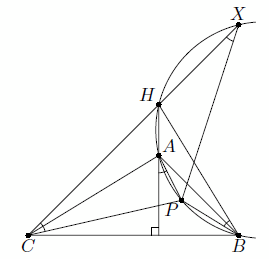
  1)  ∠(A₁A, AA_p) = ∠(B₁B, BB_p) = ∠(C₁C, CC_p)  (отсюда, в частности, следует, что треугольник ABC остроугольный; действительно, если, скажем, угол A не острый, то углы B₁BB_p и C₁CC_p острые и ориентированы по-разному). Из первого равенства следует, что точки P, H. A, B лежит на одной окружности; аналогично точка P лежит на окружностях, описанных около треугольников ACH и BCH. Но эти три окружности имеют ровно одну общую точку H; значит, P совпадает с H.  2) Два из трёх ориентированных углов равны, а третий (для определённости,  ∠(C₁C, CC_p))  им противоположен. Тогда, как и в первом случае, точкаPлежит на описанной окружности Ω_CтреугольникаABH(поскольку  ∠(AH, HB) = – ∠(AC, CB),  эта окружность симметрична описанной окружности Ω треугольникаABCотносительно прямойAB). Пусть прямаяCHвторично пересекает Ω_Cв точкеX(тогда точкиCиXсимметричны относительноAB; на рисунках показаны две таких потенциально возможных конфигурации).

  Значит,  ∠(PX, XC) = ∠(PB, BH) = – ∠(PC, CX);  если эти углы ненулевые, то это означает, что треугольникPCXравнобедренный,  PC = PX.  Но тогда точкаPлежит на серединном перпендикуляреABк отрезкуCX, что невозможно. Значит,  ∠(PB, BH) = 0,  и  P = H.   Таким образом, хорошей точкой может быть только ортоцентр треугольника (и в остроугольном треугольнике он ею, очевидно, является). Следовательно, в остроугольном треугольнике хорошая точка одна, а в неостроугольном – ни одной.

Все остроугольные треугольники.