Олимпиадная задача по комбинаторной геометрии о покрытии куба прямоугольниками Шаповалова
Задача
При каких n можно оклеить в один слой поверхность клетчатого куба n×n×n бумажными прямоугольниками 1×2 так, чтобы каждый прямоугольник граничил по отрезкам сторон ровно с пятью другими?
Решение
Куб 2×2×2 так оклеить можно (см. угловой кубик на рисунке). Если n чётно, разобьём куб n×n×n на кубики 2×2×2 и окрасим их в шахматном порядке. Заменим эти кубики на оклеенные указанным образом, причём будем располагать их так, что на верхних гранях чёрных кубиков длинные стороны прямоугольников идут в одном направлении, а на верхних гранях белых – в другом. Тогда каждый прямоугольник и будет граничить с пятью другими (см. рисунок).
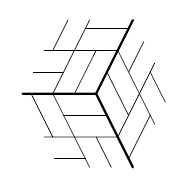
Ответ
При всех чётныхn.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет