Назад

Олимпиадная задача по планиметрии: центр вписанной окружности треугольника PQT

Задача 216910 • Сложность: 3 • 8-10 класс
Задача

Пусть AH – высота остроугольного треугольника ABC, а точки K и L – проекции H на стороны AB и AC. Описанная окружность Ω треугольника ABC пересекает прямую KL в точках P и Q, а прямую AH – в точках A и T. Докажите, что точка H является центром вписанной окружности треугольника PQT.

Авторы:
Плотников М.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина VIII Олимпиада по геометрии имени И.Ф. Шарыгина (2012 г.)
Количество версий:
5
Решение

  Пусть O – центр Ω. Из прямоугольных треугольников ABH и ACH имеем  AK·AB = AH² = AL·AC,  то есть  AK : AL = AC : AB.  Поэтому треугольники ALK и ABC подобны, то есть  ∠AKL = ∠ACB.  Поскольку  ∠OAB = 90° – ∠ACB,  то  OA ⊥ KL.  Значит, OA – серединный перпендикуляр к хорде PQ, и поэтому AP = AQ. Следовательно, TA – биссектриса угла PTQ (см. рис.).

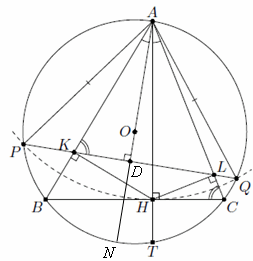
   Итак, центр I вписанной окружности треугольника PQT лежит на TA. Кроме того,  AI = AQ (см. задачу 153119).  Осталось проверить, что  AH = AP.

  Первый способ.Пусть D и N – точки пересечения AO с KL и Ω соответственно, а r – радиус Ω. Из прямоугольного треугольника AQN   AQ² = 2r·AD.  Заметим, что AH – диаметр описанной окружности треугольника AKL, значит, коэффициент подобия треугольников AKL и ABC равен  AH/2r.  Отрезки AD и AH – соответственные высоты в этих треугольниках, поэтому  AD : AH = AH : 2r,  или  AH² = 2r·AD = AQ².

  Второй способ. При инверсии с центром A и радиусом AQ прямая PQ и окружность Ω переходят друг в друга, поэтому точки B и K также переходят друг в друга. Следовательно,  AQ² = AB·AK = AH².

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет