Назад

Олимпиадная задача по планиметрии для 8–10 классов от Канель-Белова А. Я.: неравенство для выпуклого пятиугольника

Задача 216909 • Сложность: 3 • 8-10 класс
Задача

В выпуклом пятиугольнике P провели все диагонали, в результате чего он оказался разбитым на десять треугольников и один пятиугольник P'. Из суммы площадей треугольников, прилегающих к сторонам P, вычли площадь P'; получилось число N. Совершив те же операции с пятиугольником P', получили число N'. Докажите, что  N > N'.

Авторы:
Канель-Белов А. Я.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина VIII Олимпиада по геометрии имени И.Ф. Шарыгина (2012 г.)
Количество версий:
5
Решение

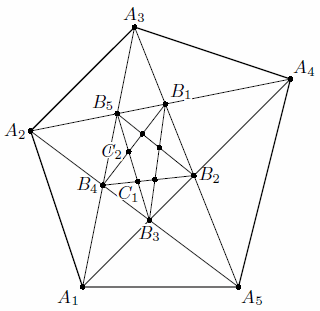
  Пусть A1A2A3A4A5 – исходный пятиугольник, B1B2B3B4B5 – пятиугольник, образованный его диагоналями, а C1C2C3C4C5 – пятиугольник, образованный диагоналями B1B2B3B4B5 (см. рис.). Продолжим нумерацию вершин циклически (то есть  Ai+5 = Ai  и т.д.).

  Заметим, что  N'= (SB1B2B3+SB2B3B4+ ... +SB5B1B2) –SB1B2B3B4B5,  поскольку в сумме справа пятиугольникC1C2C3C4C5учтён с коэффициентом –1, треугольники видаBiBi+1Ci+3– с коэффициентом 1, а треугольники видаCiCi+1Bi+3– с нулевым коэффициентом. Значит, требуемое неравенство равносильно неравенству  SA1A2B4+SA2A3B5+ ... +SA5A1B3>SB1B2B3+SB2B3B4+ ... +SB5B1B2.  Докажем, что  SAiAi+1Bi+3>SBi+2Bi+3Bi+4.    Ясно, что достаточно это доказать при  i= 1.  Присоединив к каждому из треугольниковA1A2B4иB3B4B5треугольникA1B3B4, получим треугольникиA1B3A2иA1B3B5с общим основаниемA1B3. При этом расстояние от точкиB5до этого основания меньше, чем от точкиA2; значит,  SA1A2B3>SA1B3B5.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет