Назад

Олимпиадная задача по планиметрии: радиус описанной окружности треугольника CMN

Задача 216908 • Сложность: 2 • 8-10 класс
Задача

Дан равнобедренный треугольник ABC, в котором  BC = a,  AB = AC = b.  На стороне AC во внешнюю сторону построен треугольник ADC, в котором

AD = DC = a.  Пусть CM и CN – биссектрисы в треугольниках ABC и ADC соответственно. Найдите радиус описанной окружности треугольника CMN.

Авторы:
Рожкова М.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина VIII Олимпиада по геометрии имени И.Ф. Шарыгина (2012 г.)
Количество версий:
5
Решение

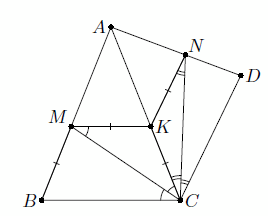
Пусть K – такая точка на отрезке AC, что  MK || BC.  Тогда  ∠MCA = ∠MCB = ∠CMK,  поэтому  MK = KC;  кроме того, из симметрии  KC = MB.  По теореме Фалеса и свойству биссектрисы  CK : AK = BM : AM = a : b = DN : AN.  Следовательно,  KN || CD;  аналогично предыдущему,  KN = KC.  Таким образом, K – центр описанной окружности треугольника CMN, а её радиус  KC = MB = ab/a+b  (см. рис.).

Ответ

ab/a+b .

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет