Олимпиадная задача по планиметрии: восстановление треугольника по точкам
Задача
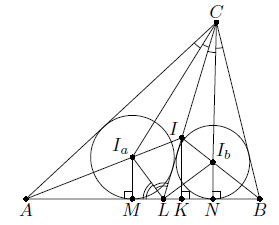
В треугольнике ABC провели биссектрису CL. В треугольники CAL и CBL вписали окружности, которые касаются прямой AB в точках M и N соответственно. Затем все, кроме точек A, L, M и N, стерли. С помощью циркуля и линейки восстановите треугольник.
Решение
Решение 1: Пусть K – точка касания вписанной окружности треугольника ABC со стороной AB (K лежит на отрезке MN). Заметим, что
MK = AK – AM = ½ (AB + AC – BC) – ½ (AL + AC – LC) = ½ (BL + LC – BC) = LN.
Пусть Ia, Ib и I – центры вписанных окружностей wa, wb и w, в треугольники ACL, BCL и ABC, соответственно. По свойству биссектрисы и теореме Фалеса имеем AL : IL = AIa : IaI = AM : MK, IL = AL·MK/AM.
Итак, мы можем последовательно построить точку K, затем I (как пересечение окружности с центром L и перпендикуляра к MN в точке K), Ia и Ib (как пересечение биссектрис углов ALI и CLI с перпендикулярами к отрезку MN в его концах), окружности wa и wb и, наконец, точки C (как пересечение касательных к wa из A и L) и B (как пересечение MN с касательной к wb из точки C).
Решение 2: Обозначим через x = AC, y = CL, z = LA длины сторон треугольника ACL, через p, S и r – его полупериметр, площадь и радиус вписанной окружности соответственно, а через h – его высоту, опущенную из вершины C; пусть ∠ACL = 2φ. Из формулы Герона 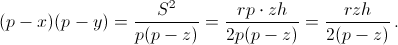
Поэтому 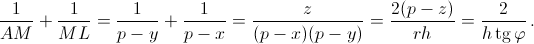 В треугольнике BCL угол при вершине C и высота из этой вершины такие же, следовательно, 1/AM + 1/ML = 1/LN + 1/NB.
В треугольнике BCL угол при вершине C и высота из этой вершины такие же, следовательно, 1/AM + 1/ML = 1/LN + 1/NB.
Таким образом, зная отрезки AM, ML, LN, мы можем найти отрезок NB и построить точку B. Из соотношений AC – CL = AM – LM и
BC – CL = BN – LN находим разность AC – BC = AM – LM – BN + LN = u, а из равенства AC/BC = AL/BL = v – их отношение. Теперь можно найти длины сторон AC = uv/v–1 и BC = u/v–1 и построить точку C.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь