Олимпиадная задача по планиметрии про треугольник и окружность для 8-10 классов
Задача
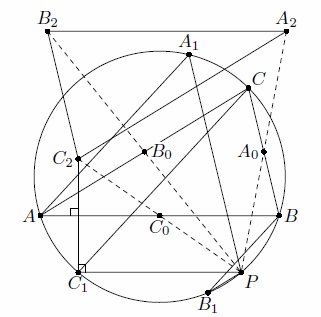
Через вершины A, B, C треугольника ABC проведены три параллельные прямые, пересекающие вторично его описанную окружность в точках A1, B1, C1 соответственно. Точки A2, B2, C2 симметричны точкам A1, B1, C1 относительно сторон BC, CA, AB соответственно. Докажите, что прямые AA2, BB2, CC2 пересекаются в одной точке.
Решение
Проведём через A1, B1 и C1 прямые a, b и c, параллельные соответственно BC, CA и AB; покажем, что они вторично пересекают описанную окружность в одной и той же точке. Действительно, пусть c пересекает окружность вторично в точке P (если она касается окружности, то P = C1). Тогда, поскольку AB || C1P и AA1 || CC1, (направленные) дуги BP, C1A и A1C равны. Это и означает, что A1P || BC, то есть a проходит через P. Аналогично b проходит через P (см. рис.).
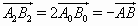 ; аналогично
; аналогично 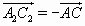 и
и 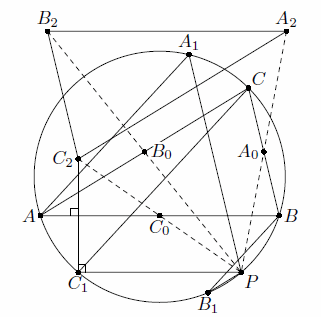 . Следовательно, треугольникиABCиA2B2C2центрально симметричны, и прямые, соединяющие их соответствующие вершины, проходят через центр симметрии.
. Следовательно, треугольникиABCиA2B2C2центрально симметричны, и прямые, соединяющие их соответствующие вершины, проходят через центр симметрии.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь