Назад

Олимпиадная задача по планиметрии из треугольника с высотами (8–10 класс)

Задача 216903 • Сложность: 2 • 8-10 класс
Задача

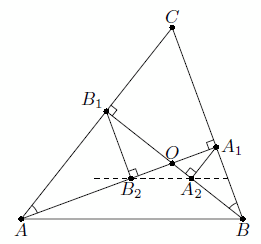
В остроугольном треугольнике ABC провели высоты AA1 и BB1, которые пересекаются в точке O. Затем провели высоту A1A2 треугольника OBA1 и высоту B1B2 треугольника OAB1. Докажите, что отрезок A2B2 параллелен стороне AB.

Авторы:
Штейнгарц Л.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина VIII Олимпиада по геометрии имени И.Ф. Шарыгина (2012 г.)
Количество версий:
4
Решение

Прямоугольные треугольники OA1B и OB1A подобны (см. рис.). Значит, их высоты A1A2 и B1B2 делят отрезки OB и OA в одном и том же отношении. Отсюда по обратной теореме Фалеса получаем утверждение задачи.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет