Олимпиадная задача по планиметрии для 8-9 класса: ∠QPH = 90° в остром треугольнике

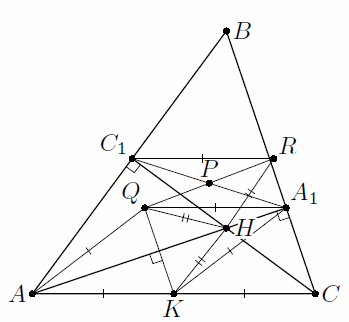
Решение 1:   Пусть K – середина AC. Так как  KQ || BC,  то KQ делит высоту AA₁ пополам. Значит, в четырёхугольнике AKA₁Q диагонали перпендикулярны и делятся точкой пересечения пополам, то есть он – ромб. Кроме того, из симметрии  HQ = HK.

  Аналогично пусть R – точка, симметричная K относительно CC₁; тогда CKC₁R – ромб, и  HQ = HR  (рис. слева). Значит, отрезки A₁Q, AK, KC и C₁R параллельны и равны, откуда QA₁RC₁ – параллелограмм. Следовательно, P – середина RQ, а HP – медиана (а значит, и высота) равнобедренного треугольника HQR.

           

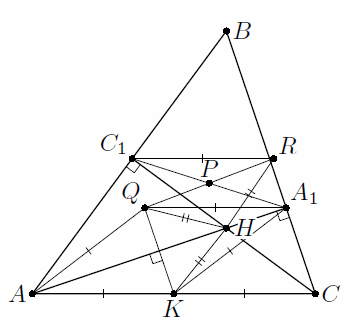
Решение 2:   Пусть L – середина AA₁. Тогда PL – средняя линия треугольника AA₁C₁,  поэтому  ∠PLH = ∠BAA₁ и, следовательно,  ∠PLQ = 90° – ∠PLH = ∠C₁HA.  С другой стороны, точки A₁ и C₁ лежат на окружности с диаметром AC, поэтому треугольники A₁C₁H и CAH подобны. Значит, их медианы HP и HK образуют равные углы со сторонами HC₁ и HA соответственно (рис. справа). Отсюда  ∠QHA = ∠KHA = ∠PHC₁,  и поэтому  ∠PHQ = ∠C₁HA = ∠PLQ.  Следовательно, точки P, Q, L, H лежат на одной окружности и  ∠QPH = 180° – ∠QLH = 90°.

Ответ задачи отсутствует