Олимпиадная задача по планиметрии: ортоцентр и окружность, 8-9 класс, автор Туманян А.
Задача
Окружность Ω описана около треугольника ABC. На продолжении стороны AB за точку B взяли такую точку B1, что AB1 = AC. Биссектриса угла A пересекает Ω вторично в точке W. Докажите, что ортоцентр треугольника AWB1 лежит на Ω.
Решение
Пусть H – вторая точка пересечения Ω с прямой CB1. Поскольку AW – биссектриса равнобедренного треугольника AB1C, то B1H ⊥ AW. Если точки C и W лежат по одну сторону от AH, то ∠AWH = ∠ACH = 90° – ∠CAW = 90° – ∠WAB, то есть WH ⊥ AB1 (см. рис.). Если они лежат по разные стороны, то ∠AWH = 180° – ∠ACH = 90° + ∠WAB, откуда опять же следует, что WH ⊥ AB1. Наконец, если эти точки совпадают, то треугольник AWB1 прямоугольный, и H = W – его ортоцентр. В любом случае точка H лежит на двух высотах треугольника AWB1, то есть является его ортоцентром.
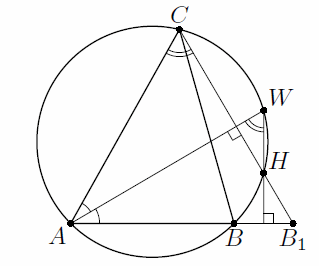
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь